Math

My favorite math problem

What is your favorite math topic/problem? I've been asked this in interviews as well as in general conversation (yes, that says something about the kind of people I'm conversing with). While there are some advanced theorems that I think are impressive, I eventually settled on the following:

I picked this because there are surprisingly many contexts in which that expression appears. I've put several below, but I'm sure there are even more.

• Addition

  Often, the first place students encounter this expression (if they encounter it at all) is as a forumula for $1 + 2 + 3 + \cdots + n$. There are many explanations as to why this sum has the value $\frac{n(n+1)}{2}$. Just a few are described below.

• Apocryphal history

  There are many stories about how brilliant Carl Friedrich Gauss (1777-1855) was at a young age. One such story is that to keep Gauss busy and quiet during school, his teacher gave him the task of adding all the whole numbers from $1$ to $100$. The teacher was amazed when Gauss produced the answer ($5050$) within seconds.

  This story is probably not true. However, it is not hard to explain at the level of a child how the sum can be done so quickly. Writing out the numbers in a two-row “snake” as

  $1$	$2$	$3$	$4$	$5$	⋯	$48$	$49$	$50$
  $100$	$99$	$98$	$97$	$96$	⋯	$53$	$52$	$51$

  one sees that in each column the two numbers add to exactly $101$. Since there are $50$ columns, this gives the total sum as $50 \times 101 = 5050$. The same argument can be applied to

  $1$	$2$	$3$	⋯	$\frac n2 - 2$	$\frac n2 - 1$	$\frac n2$
  $n$	$n-1$	$n-2$	⋯	$\frac n2 + 3$	$\frac n2 + 2$	$\frac n2 + 1$

  for any even $n$, and a slight modification can handle odd $n$ as well.

• Induction

  This is one of the standard examples of a formula that can be proved by mathematical induction. Since it can also be proved several other ways, one can see that induction confirms the result already known to be correct.

  Claim: $1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2}$ for all natural numbers $n$.

  Base case: for $n = 1$, it is true that $1 = 1$.

  Inductive step: Assume that $1 + 2 + 3 + \cdots + k = \frac{k(k+1)}{2}$. Then \begin{align*} 1 \!+\! 2 \!+\! \cdots \!+\! k + (k\!+\!1) &= \frac{k(k+1)}{2} + k+1 \\ &= \frac{k(k+1)}{2} + \frac{2(k+1)}{2} \\ &= \frac{k(k+1) + 2(k+1)}{2} \\ &= \frac{(k+1)(k+2)}{2} \end{align*} These algebra steps show that if the formula works for some value $k$ then it also works for $k+1$. And we know the formula works for the base case $1$. Therefore the formula is true for all natural numbers $n \ge 1$.

• Geometry

  The values \begin{align*} {\bf 1} &= 1, \\ {\bf 3} &= 1 + 2, \\ {\bf 6} &= 1 + 2 + 3, \\ {\bf 10} &= 1 + 2 + 3 + 4, \\ {\bf 15} &= 1 + 2 + 3 + 4 + 5, \end{align*} etc., are called triangular numbers because they are the number of dots in the following triangular arrangements: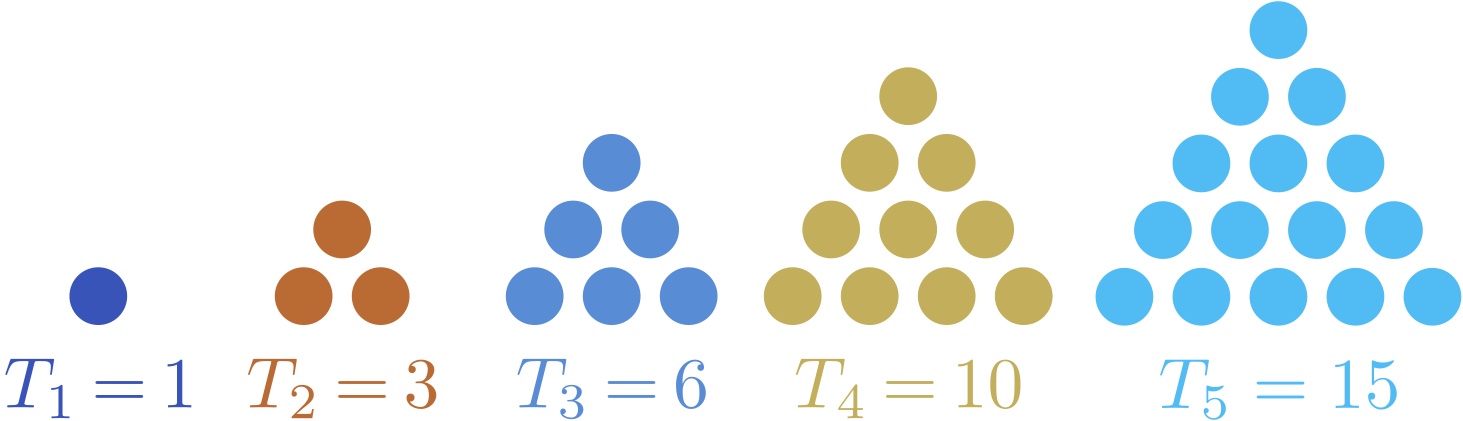

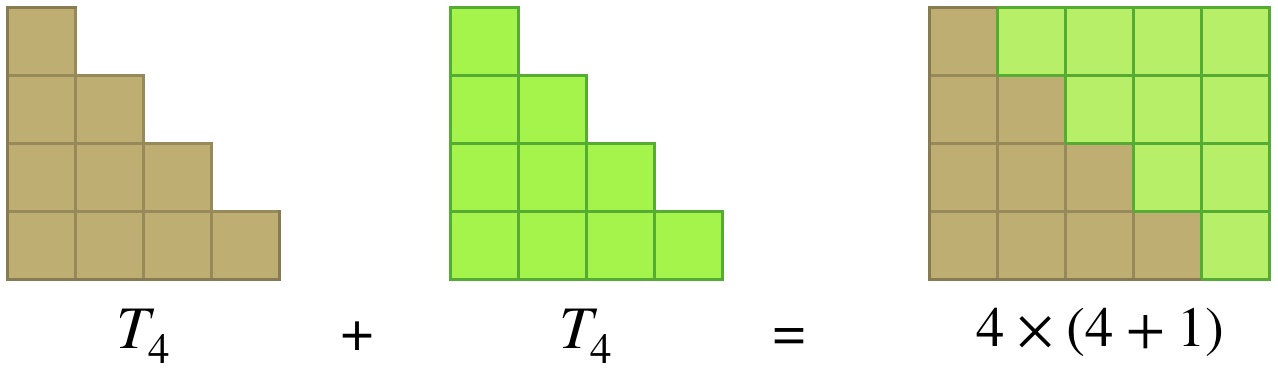
  If we denote by $T_n$ the number of dots in a triangle with $n$ rows, we have that $T_n = \frac{n(n+1)}{2}$. Note that we've already proven this since adding the dots in each row of the triangle gives $1+2+3+\cdots$, but this geometric description of what $T_n$ means leads to a nice geometric proof. Drawing our triangles as right triangles made of boxes, we can fit two copies of $T_n$ together into a rectangle. For $n=4$ this looks like
  

  and we see that $T_4 + T_4 = 4 \times 5$. In general, we get that $T_n + T_n = n \times (n+1)$ becuase the rectangle will have $n$ rows and $n+1$ columns. Dividing both sides of this equation by $2$ gives us $T_n = \frac{n(n+1)}2$.

• Combinatorics

  Suppose there are $100$ different books in a bag, and you want to choose two of them (order doens't matter); how many ways are there to do this? The idea of choosing objects without order is so common that it has many different notations. In this case the answer could be written as any of \[ \textstyle {}_{100}C_2 \qquad {}^{100}C_2 \qquad \binom{100}{2} \qquad C(100,2), \] but this value is not new: it is exactly $T_{99}$.

  This is actually pretty easy to see if you reformulate the problem as “How many distinct handshakes can take place between $100$ people?” You could think of the choosing two people to shake hands, and there are $_{100}C_{2}$ ways to make this choice. On the other hand, you can start by having one person shake hands with all $99$ others, then have another person shake all $98$ hands they haven't shaken yet (it's only $98$ because they already shook hands with the first person), then the next has $97$ to do, then so on to $\cdots + 3 + 2 + 1$. So this is indeed $T_{99}$.

  In general, we have that $T_n = {}_{(n+1)}C_{2}$.

• Perfect numbers and Mersenne primes

  Every even perfect number is triangular, as first proved by Euler in 1849. A whole number $N$ is called perfect if the proper factors of $N$ (that is, the factors not including $N$ itself) add up to exactly $N$. For example, $28$ is perfect because its factors are $\{1,2,4,7,14,28\}$ and $1+2+4+7+14 = 28$. Note that $28 = T_7$.

  You may note that I said every even perfect number is triangular. What about odd perfect numbers? Well, it turns out that no one has been able to prove whether there are any odd perfect numbers! No one has found any (computers have tested up to $10^{1500}$), and there are heuristic arguments as to why probably none exist, but as of 2024 there is no formal proof that there are no odd perfect numbers.

  Not all triangular numbers are perfect, so one may wonder, “For which $n$ is $T_n$ perfect?” The answer: $T_n$ is perfect if $n$ is a Mersenne prime, that is, a prime of the form $2^p - 1$. From now on, we denote $M_p = 2^p-1$.

• Ancient history

  The fact that $T_{M_p}$ is perfect when $M_p = 2^p - 1$ is prime was proved by Euclid around 300 BCE, which I find particularly fascinating because Euclid primarily did geometry. He would never write $2^p$ since the idea of using superscripts for exponents comes from Descartes in the 1600s. And he wouldn't even write $n(n+1)/2$ because using letters for variables wasn't common until in the 1500s. Elements Book IX, Proposition 36 states...

  “If as many numbers as we please beginning from a unit are set out continuously in double proportion, until the sum of all becomes prime, and if the sum multiplied into the last make some number, then the product will be perfect.”

  In modern notation, this says that if $1 + 2 + 4 + 8 + \cdots + 2^k$ is prime, then $(1+2+4+\cdots+2^k)2^k$ is perfect. The sum $1+2+4+\cdots+2^k$ is exactly $2^{k+1}-1$ (this can be shown easily if you are comfortable writing the numbers in binary), and the last term $2^k$ can be written as $\frac{2^{k+1}}2$, so if we set $n=k+1$ we have

  If $2^n-1$ is prime then $\frac{(2^n-1)2^n}2$ is perfect.

  or, using our notation for triangular and Mersenne numbers,

  If $M_n$ is prime then $T_{M_n}$ is perfect.

  The converse—if $N$ is perfect then $N = T_{M_n}$ for some $n$—was suspected for centuries and finally proved by Euler in 1849.

• Open problems

  As mentioned, it is not known whether any odd perfect numbers exist at all. What about even perfect numbers? As of 2024, we know exactly $50$ perfect numbers, which means we also know exactly $50$ Mersenne primes too, but it is still unknown whether there are infinitely many of them.

  Admittedly, these problems are not exactly about triangular numbers $T_n$ but rather about perfect numbers and Mersenne primes $M_p$, yet since every even perfect number is $T_{M_p}$ for some $p$, it is still related.

• Correcting history

  The story about Gauss adding $1$ through $100$ may or may not be true, but there is some interesting history regarding Marin Mersenne himself and his namesake primes. In the 17^th Century, Mersenne listed the following as values of $p$ for which $2^{p}-1$ is prime: \[ 2,\quad 3,\quad 5, 7,\quad 13,\quad 17,\quad 19,\quad 31,\quad {\color{red}{67}},\quad 127,\quad {\color{red}{257}}. \] Aside from missing that $M_{61}, M_{89}, M_{107}$ are prime, this list incorrectly includes $M_{67}$ and $M_{257}$, which are not prime. In 1876, Édouard Lucas showd that $M_{67}$ was composite but did not find explicit factors.

  In 1903, Frank Nelson Cole gave a completely silent presentation to the American Mathematical Society in which he calculated entirely by hand \[ 2^{67} - 1 = {{147,\!573,\!952,\!589,\!676,\!412,\!927}} \] on one part of a blackboard and on another multiplied out \[ {{193,\!707,\!721}} \times {{761,\!838,\!257,\!287}} = {{147,\!573,\!952,\!589,\!676,\!412,\!927}} \] by hand. He then returned to his seat, still without speaking, and recieved a standing ovation.